by R. Grothmann
I want to compute the famous curve, which appears as a polar set of a ladder with fixed length, leaning at a wall (see the image below).
If a is the height of the ladder at the wall, then sqrt(1-a^2) is the distance of the foot from the wall (assuming the ladder has length 1), and we get the following equation for the line.
>eq &= y/a+x/sqrt(1-a^2)=1
y x
- + ------------ = 1
a 2
sqrt(1 - a )
We can solve this equation for y, and get the equations of a set of lines.
>&solve(eq,y), function y(x,a) &= y with %[1]
2
a sqrt(1 - a ) - a x
[y = --------------------]
2
sqrt(1 - a )
2
a sqrt(1 - a ) - a x
--------------------
2
sqrt(1 - a )
The maximal height at each x is the curve, we are looking for (the envelope). So we try to find it, making sure to pick the correct solution.
>&assume(x>0); sol &= solve(diff(y(x,a),a)=0,a)
2/3 2/3
sqrt(sqrt(3) I x + x + 2)
[a = - -------------------------------,
sqrt(2)
2/3 2/3
sqrt(sqrt(3) I x + x + 2)
a = -------------------------------,
sqrt(2)
2/3 2/3
sqrt(- sqrt(3) I x + x + 2)
a = - ---------------------------------,
sqrt(2)
2/3 2/3
sqrt(- sqrt(3) I x + x + 2) 2/3
a = ---------------------------------, a = - sqrt(1 - x ),
sqrt(2)
2/3
a = sqrt(1 - x )]
>function f(x) &= factor(at(y(x,a),sol[6]))
2/3 1/3
sqrt(1 - x ) (x - x )
- -------------------------
1/3
x
There is the following parametrization of the curve.
![]()
>&assume(cos(t)>0); &trigsimp(f(sin(t)^3))
3
cos (t)
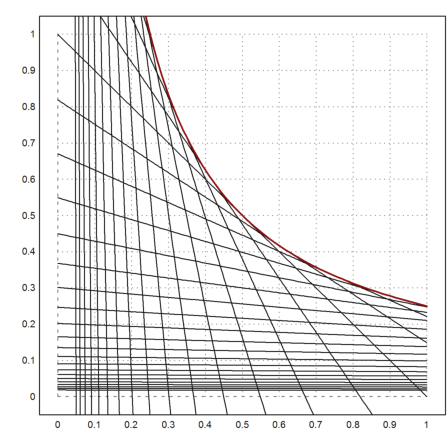
Now we plot everything, first the ladders.
>a=(0.1:0.05:0.9)'; plot2d("y(x,a)",a=0,b=1,c=0,d=1):
Then the function.
>plot2d("f",add=1,color=2,thickness=2):
We can use the very same code to study other functions, like the segments, such that the y-abscissa plus the x-abscissa are constant.
>eq &= y/a+x/(1-a)=1
y x
- + ----- = 1
a 1 - a
We can solve this equation for y, and get the equations of a set of lines.
>&assume(x>0); ... &solve(eq,y); function y(x,a) &= y with %
2
a x + a - a
------------
a - 1
The maximal height at each x is the curve, we are looking for (the envelope). So we try to find it, making sure to pick the correct solution.
>&solve(diff(y(x,a),a)=0,a), function f(x) &= factor(y(x,a) with %[1])
[a = 1 - sqrt(x), a = sqrt(x) + 1]
3/2
x - 2 x + sqrt(x)
--------------------
sqrt(x)
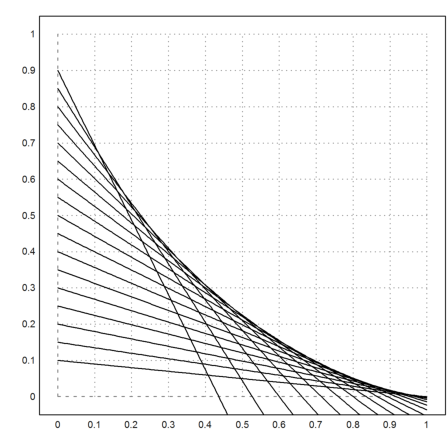
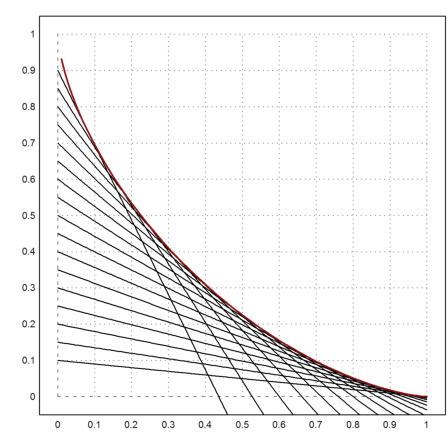
Now we plot everything, first the ladders.
>a=(0.1:0.05:0.9)'; plot2d("y(x,a)",a=0,b=1,c=0,d=1); ...
plot2d("f",add=1,color=2,thickness=2):
Here is another example wheret the y-abscissa times the x-abscissa is constant.
>eq &= y/a+a*x=1
y
- + a x = 1
a
We can solve this equation for y, and get the equations of a set of lines.
>&solve(eq,y); function y(x,a)&=rhs(%[1])
2
a - a x
The maximal height at each x is the curve, we are looking for (the envelope). The result is very simple this time.
>&assume(x>0); ... &solve(diff(y(x,a),a)=0,a), function f(x)&=factor(at(y(x,a),%[1]))
1
[a = ---]
2 x
1
---
4 x
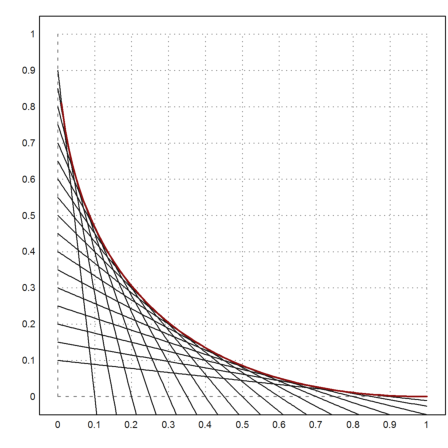
Now we can plot everything.
>a=exp(-4:0.2:4)'; plot2d("y(x,a)",a=0,b=1,c=0,d=1); ...
plot2d("1/(4*x)",add=1,color=2,thickness=2):